
A
short guide
August
2007
PeakDetection,
<peakdet>, is a MatLab script for calculating
fundamental frequency (the inverse of glottal cycle length) and glottal
open
quotient from electroglottographic signals.
New to 2007: visual indication on voice
onset and
voice offset
<peakdet>
now shows
the position of the first and last detected glottis-closure-instants on
the
electroglottographic signal and on its derivative (=figures 2 and 3),
so that
the user can appraise visually whether the full interval of voicing has
been
taken into account or not. This is useful in cases where the amplitude
of the
signal varies considerably within the portion of signal under analysis.
(See
lines 197-218 of <peakdet.m>.)
The
duration of glottal cycles is measured by detecting positive peaks on
the derivative
of the electroglottographic signal (hereafter DEGG). The inverse of
this
duration is still called « fundamental
frequency » for short, but
there is no check on periodicity, as peaks are detected individually.
This is
different from correlation-based methods (such as DECOM: Henrich
et al. 2004).
To
avoid
absurd results in the case of double closing peaks, a threshold on
maximum
fundamental frequency is set by the user, and peaks that are so close
that the
corresponding F0
is above
this threshold are considered as belonging in the same ‘peak
cluster’.
In
light of
the great differences in F0 range across speakers and across the
experimental
tasks that they perform, it did not appear adequate to set the same
threshold
for all speakers (say, 500 Hz): the user must be allowed to
modify the
threshold.
It
was not
found useful to set a lower threshold parallel to this upper threshold.
Implausibly low values in the results point to one of the following
situations :
-
one
closing peak has been detected before the onset of
voicing or after the offset of voicing, resulting in the detection of a
‘period’ the inverse of which is under 20 Hz. These
cases can be corrected by
suppressing the first or last period ; this option is offered
by the
program, at the stage where the user is asked to check the results.
-
some
closing peaks within a voiced portion of signal
have gone undetected because their amplitude is below the threshold.
The user
must then check on the figure which amplitude threshold is to be chosen
for all
the peaks to be detected, and set the amplitude threshold
accordingly ;
this option is offered by the program when the user is asked to confirm
the
results.
Smoothing
the DEGG signal turned out to be useful in the many cases where there
is one
single opening peak but its amplitude is very small and it tends to be
drowned
in noise. The <peakdet> programme smoothes the DEGG
signal as follows,
where <C_SMOO> is the smoothing step and
<dSIG> the derivative
(two-point derivative) of the EGG signal :
% filling first and last values
with original values
for i = 1 : C_SMOO
SMOO_dSIG(i) = dSIG(i);
SMOO_dSIG(length(dSIG) + 1 -
i) =
dSIG(length(dSIG) + 1 - i);
end
% smoothing
for i = 1 + C_SMOO : length(dSIG) - C_SMOO
SMOO_dSIG (i) = sum(dSIG(i -
C_SMOO:i +
C_SMOO)) / (2 * C_SMOO + 1);
end
This
amounts to : a smoothing step of 1 means smoothing 1 point to
the left and
right, i.e. each point in <SMOO_dSIG> is the average of 3
points in
<dSIG> ; 2 means averaging over (2x2+1) = 5
points.
As
the
programme computes the open quotient results by four methods two of
which
operate on the unsmoothed signal, it is avisable to choose a smoothing
step (of
1) even if the user believes that this smoothing is
unnecessary : this
assumption can be verified by comparing the results with and without
smoothing,
which will show a complete fit if the original signal has very little
background noise.
Concerning
the choice of a smoothing step for noisy signals : a step up
to 5 can be
chosen ; visual comparison of the DEGG signals before and
after smoothing
is recommended to verify that this smoothing does not make neighbouring
peaks
coalesce. It must be remembered that in some cases the DEGG method
simply does
not apply, and (arguably) should not be forcibly applied : if
taken to its
limits, smoothing artificially creates a neat hump for opening and one
for closing,
but these humps fudge up the issue, as they do not correspond to any
precise
physiological reality anymore : the advantage of the DEGG
method is that
it is based on an established relationship between the DEGG signal and
significant glottal events ; extreme smoothing blurs this
relationship.
In
a
nutshell : a smoothing step of 1 is adequate for high-quality
signals
(which already appear visually as very smooth), a smoothing step of 2
or 3
increases correct peak detection in relatively noisy signals.
Fudging-up of
opening peaks was only observed with a smoothing step of 6 or more.
<peakdet>
functions semi-automatically : it allows the user to choose
which open
quotient results can be retained, on the basis of relevant
information :
the shape of the signals, and the results of four calculation methods
for open
quotient. The methods are divided into two sets :
-
detection
of the local minimum on the signal
in-between two closure peaks ; this method is applied
twice : on the
unsmoothed DEGG signal, and on the smoothed DEGG
-
analysis
of the shape of opening peaks and calculation
of a barycentre of the detected
‘peaks-within-the-peak’, giving each of the
peaks a coefficient proportional to its amplitude. Again, this method
is
applied twice : on the unsmoothed DEGG signal, and on the
smoothed DEGG.
The
minima
method does not take into account the shape of the peak. The barycentre
method
is sensitive to every change of the sign of the second derivative of
the EGG
signal, i.e. to every dent in the signal.
Our
experience is that detection of the local minima on the smoothed DEGG
signal
in-between two closure peaks gives precise and satisfactory results in
most
cases. The barycentre method can be used as a check : if there
is a good
fit between its results and those obtained by the minima method, the
user can
confidently assume that the opening peak stands out clearly, and is not
dented ; if its results are different, this means that the
peak is dented
or double, calling for verification by inspection of the signals, and
most
likely for elimination of open quotient values. This is exemplified in
the
figures below. Figure 1 shows open quotient results calculated by the
four
methods. The open quotient curve is reasonably continuous. It starts
from a
very high value (above 80%), which is frequent after aspirated
consonants ; it then goes down to about 55%. The last value is
not
plausible because there is a sudden jump ; so it calls for
confirmation.

The
blue line,
corresponding to the values calculated by detecting the minima on the
smoothed
signal, coincides almost entirely with the green asterisks
corresponding to
detection on the unsmoothed signal, whereas there is a difference (on
the order
of 2%) between the minima methods and the barycentre methods, the
latter
yielding lower open quotient values.
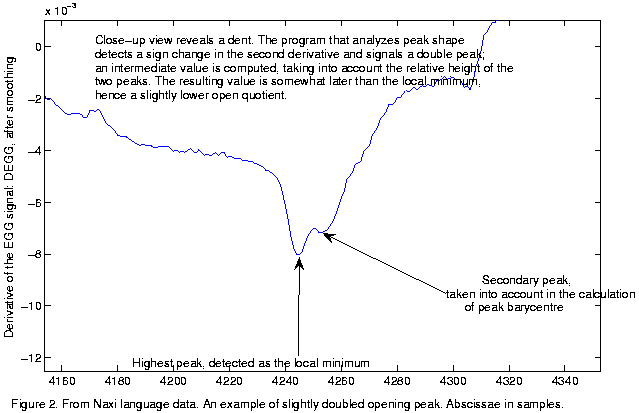
The
explanation can be found by inspecting the DEGG signal, presented and
commented
on in figure 2, which shows a close-up view of one of the opening peaks
in the corresponding
DEGG signal : there is a dent in the signal, the main peak
being followed
by another peak of smaller amplitude. An intermediate value is computed
by the
barycentre-method algorithm ; as the secondary peak comes
later, the open
quotient is slightly lower. On the basis of these observations, the
user may
decide
-
to
retain the values calculated by minima detection,
considering that they offer a coherent result and that the main peak is
salient
enough to be chosen as indicative of the timing of glottal opening
-
to
retain the values calculated by barycentre, which
reflect the asymmetrical shape of the peak
-
or
to exclude all values, considering that the peak is
not unique, strictly speaking, which disallows the calculation of a
single
value of « time of glottal
opening » on which to base an open
quotient calculation.
The
final
choice will depend on the objective of the study, and the degree of
precision
required to demonstrate the hypotheses at issue. If, for instance, the
hypothesis was the absence of glottal constriction on the rhyme type
illustrated by this example, the experimental uncertainty on the order
of 2%
would have no importance : all the measurements coincide to
indicate that
open quotient is near its average value (this observation must of
course be
refined by proposing speaker-specific reference values) and that there
is no
tendency to glottal constriction. It would therefore be advisable to
include
these results despite the slight asymmetry in the shape of the opening
peak. On
the other hand, if the focus is on differences in open quotient across
vowels
(‘intrinsic open quotient’), the expectation is
that these differences will be
small, and an experimental uncertainty on the order of 2% may not be
acceptable.
The
choice
also depends on the quality and abundance of the EGG data. If there are
sufficiently numerous cases where there is an excellent fit among
methods, it
seems reasonable to isolate all the doubtful cases, treating them as a
separate
set or excluding them altogether.
This
part
of the work is therefore of great importance, and the user should be as
explicit as possible concerning the criteria used.
One
example
in which open quotient calculation is problematic is shown in figure 3.

The
dispersion of the values obtained by the barycentre method hints at
imprecise
or multiple opening peaks. None of the methods yields a continuous
curve of
open quotient. It is necessary to exclude all the open quotient values
on the
second half of the item. On the first half of the item, the results
obtained by
the minima method applied to the smoothed DEGG signal are not absurd,
and are
in some degree continuous. It is therefore useful to have a look at the
shape
of the corresponding DEGG signal : see figure 4, which
represents one of
the first periods. The peak is strongly dented ; the dents are
detected as
so many peaks, which results in displacing the barycentre of peaks in a
way
that varies strongly from one syllable to the next. On the whole,
however,
there is no clear doubling of the opening peak (which would mean the
presence
of two peaks of comparable amplitude). This offers an argument for
retaining
(for the first periods) the open quotient values calculated by the
minima
method ; the interval over which these results can be retained
approximately
covers periods 3 to 14. The values for the first two periods, and for
the
periods after period 15, positively have to be excluded, as there is no
salient
opening peak. (The choice that we made when treating these data
consisted in
excluding all the open quotient values, in view of the general
variability of
the results. If the user chose to retain values 3 to 14, it should be
reported
that the results are doubtful.)

Figure
5
below exemplifies a frequent situation : the overall fit
across methods is
good ; the results from the methods applied on the unsmoothed
signal
contain a few out-of-range values, which are corrected in the results
using the
smoothed signal, indicating that the quality of the EGG recording is
acceptable
but not ideal.


Examination
of the signal shows that detection of opening peaks is not problematic,
though
the fine detail of the DEGG signal is not smooth ; this is a
case where it
could be useful to increase the smoothing step.
In
this
case, the values in blue (calculation on the smoothed signal :
detection
of the minima) were chosen, only excluding the value on period 9
because it is
higher than its neighbours and the corresponding peak in the signal is
not
clear.
Figures
7
and 8 show an example in which the barycentre method yields a
continuous open
quotient curve despite peak doubling. The curve in blue is
saw-like : its
lack of smoothness indicates that the measurement was not successful,
probably
due to the fact that the opening peak is doubled or imprecise. The
values
obtained by barycentre method (black squares) show slightly greater
continuity.

Examination
of the DEGG signal (figure 8) shows that this is a case of peak
doubling. In
this instance, the barycentre method appears as an acceptable
compromise in
case one chooses to provide an approximation of the open quotient
despite the
absence of a clear, single opening peak. Here again, the final choice
(excluding all open quotient values or not) depends on the degree of
precision
required.

Lastly,
figure 9 (next page) illustrates the excellent fit across methods that
is
obtained when the opening peaks stand out clearly, and the
corresponding DEGG
signal. In such a case, our choice is to select the method by detection
of
minima on the smoothed signal (results in blue) ; the choice
of this
method as a default method of sorts is reflected in the choice to plot
it as a
stars-plus-line curve, the better to make its continuity (or lack of
such)
stand out.

There
are
comments within the text of the main program, <peakdet>,
as well as in
all the functions.
In
its
present version, <peakdet> requires a .wav file as its
input. If there is
more than one channel, <peakdet> expects the EGG signal
to be in the
second channel (right channel of stereo files). If your files are in
another
format, you can either convert them, or modify <peakdet>
using another
function such as <allread> for loading the data.
The
beginning and end of the portions of the signal to be treated should be
provided either (i) as a .txt file containing the beginning
and end of
each item (in milliseconds), or (ii) as a .txt file produced
from a
Regions List of the software SoundForge (©SonicFoundry). Here
are some details:
(i) The
input can be a .txt file containing the beginning and end of each item
(in
milliseconds) on one single line, separated by spaces or tabs, e.g.
2963 3471
7662 8428
11853 12561
16594 17031
20863 21466
If
there
are more than 2 columns the software retains the last 2, e.g.
1
2963 3471
2
7662 8428
3
11853 12561
4
16594 17031
5
20863 21466
will
be
read in the same way as the lines above. This allows you to give the
items a
number for identification.
(ii) The
input can be a .txt file produced from a Regions List of the software
SoundForge®. The reason why we did a conversion module
specifically for the
latter, and not for other formats of annotation, is because we used
SoundForge
to create the annotation to our EGG files, and needed to be able to
make the
conversion easily. After doing the annotation in SoundForge, copy it to
the
Clipboard then to a .txt file.
This
file
is read and converted by the function <beginend> called
by
<peakdet>.
When
you
run <peakdet>, it first asks you to set a few parameters
and indicate the
path to the .wav file and the .txt file. Then it analyzes the intervals
indicated in the .txt file, one by one, asking you to validate the
results
syllable by syllable ; you can correct the results manually in
several
ways, suppressing the first or last period, correcting F0 values
manually, and
suppressing open quotient values that are out of range or correspond to
passages where the open quotient cannot safely be calculated. The
result is
placed in a matrix called <data>, containing one sheet
per item analyzed,
and padded with zeros. Have a look at the <peakdet>
program to see how
each sheet is organized ; basically : F0 is in the 3rd
column, and the open quotient values retained are in the 10th
column.
If
you have any questions or suggestions please contact
alexis.michaud@cnrs.fr
Reference
cited:
Henrich,
N.; d'Alessandro, C.; Castellengo, M.; Doval,
B.: On the use of the derivative of electroglottographic signals for
characterization of non-pathological voice phonation. Journal of the
Acoustical
Society of America 115(3):
1321-1332
(2004).